As name suggest, A sum of products expression contains the sum of different terms, now each term may be either a single literal or a product of more than one literal. Now take a simple example. Let A, B and C are the different literals of a binary system. Now those literals may connected each other in different combination (maximum 8 combination) by the relation of product with each other’s like ABC, ABC^, AB^C, AB^C^, A^BC, A^BC^, A^B^C, A^B^C^. So out of those input product combination creating by literals some of produce logic ‘1’ at the output. It can be easily obtained from the truth table directly by considering those input combinations that produce logic ‘1’ at the output. Each such input combination which produces logic ‘1’ at output is called a term. Now any expression where the different terms are interrelated by summation with each other is called sum of products expression.
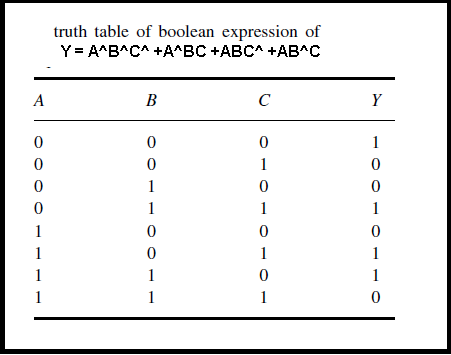
Let take an example of sum of products expression of three literal A, B and C. Now see the truth table of A, B and C literal for any digital system.
From this above truth table we can get the sum of products expression is
Y = A^B^C^ +A^BC +ABC^ +AB^C.
Considering the first term, the output is ‘1’ when A = 0, B = 0 and C = 0. This is possible only when A^, B^ and C^ are ANDed. Also, for the second term, the output is ‘1’ only when B, C and A^ are ANDed.
Other terms can be explained similarly. A sum-of-products expression is also known as a minterm Expression